Переливания

Е. М. Шамахова

Здравствуйте, друзья! Я очень рада новой встрече!

Сейчас открою дверь МатеМаше и ПрограМише – они снова пришли в гости – и мы вместе отправимся на поиски интересных задач.
— Здравствуйте, Евгения Михайловна! – выпалил ПрограМиша, как только я открыла дверь. — А что мы будем решать сегодня?
— Сегодня будем переливать, — ответила я.
— Что переливать?
— Воду.
— Куда и откуда? И зачем? – удивилась МатеМаша.
— Будем решать задачки, в которых нужно переливать воду. Точнее, нужно с помощью имеющихся емкостей набрать из речки нужное количество воды.
— Здорово! Пойдемте скорее на речку! – подпрыгнул от восторга ПрограМиша.
— Нет, идти никуда не придется, достаточно лишь напрячь фантазию, — остановила я ПрограМишу, но, кажется, это совсем не испортило его настроения, ПрограМиша большой любитель пофантазировать.
— Вот вам первая задача:

Задача 1.
У нас есть два ведра емкостью 3 литра и 5 литров. С помощью этих ведер нужно набрать из речки ровно 4 литра воды.

— Ну и что же тут сложного? – удивился ПрограМиша, — сейчас я запросто наберу. Сначала наберу 3 литра, перелью в пятилитровое ведро, а потом налью в трехлитровое треть ведра – вот и получится 4 литра.
— А как ты отмеришь эту треть, чтобы было ровно-ровно? – спросила МатеМаша. Ей это действие внушало какое-то недоверие, только она не могла его объяснить.
— Действительно, а как ты отмеришь ровно треть? — поддержала я МатеМашу. – На трехлитровой емкости нет никаких делений, а форма емкости может быть такой замысловатой, что по ней очень трудно понять, где будет ровно треть.
— Не знаю, — сдался ПрограМиша. Он хоть и любил поспешить, но быстро соглашался, если действительно оказывался неправ.
— У меня есть идея, — задумчиво предложила МатеМаша. – Что если набрать в каждое ведро ровно половину… Можно я буду называть емкости ведрами?
— Можешь называть ведрами, если тебе так проще, но помни, что форма этих ведер может быть какая угодно, — только успела сказать я, как меня перебил ПрограМиша.
— А как ты собираешься отмерить ровно половину? Разве это легче, чем отмерить треть? Половина тоже нигде не нарисована.
— Есть одна идея, — МатеМаша взяла с моего стола стакан. – Кажется, я где-то читала, что если налить в стакан воду и наклонить его так, чтобы уровень воды шел точно по диагонали от верхнего уголка, как бы касаясь края стакана, а с другой стороны как будто упирался одной точечкой в дно, то будет ровно половина.

Если я сделаю так же с ведрами, то получу в одном ведре полтора, а в другом два с половиной литра, а в сумме это как раз и получится 4 литра, потому что целых литров будет 3, а две половинки как раз и дадут еще один целый литр.
— Это интересная идея, — похвалила я, — но она подойдет, только если оба ведра круглой цилиндрической формы, то есть круглые с абсолютно ровными краями, одинаковые сверху и снизу. А если, например, ведро расширяется кверху, то таким методом мы уже не получим ровно половину. Не говоря уже о том, что наши емкости могут иметь и более замысловатую форму.
— Жаль, — задумчиво сказал ПрограМиша, ему явно понравилась идея МатеМаши.
— Давайте немножко уточним, что мы подразумеваем в таких задачах, — решила пояснить я. – Форма емкостей специально считается совсем неправильной и непонятной, чтобы мы знали, что такой емкостью точно можно отмерить только такое количество воды, которое в ней помещается, если наполнить ее целиком. Ну и, конечно, мы считаем, что при переливаниях из одной емкости в другую мы переливаем абсолютно всю воду, не теряя ни капельки, то есть не разбрызгиваем, на стенках ведра как будто бы ничего не остается, и так далее. Понятно?
— Понятно, — дружно ответили дети, — в математике мы часто с таким встречается: фигуры считаем идеально ровными, а не как мы обычно рисуем в тетрадках, вычисляем всегда точно, а не примерно, как иногда делаем в магазине.
— Точно. Ну тогда попробуйте попереливать еще, чтобы получить ровно 4 литра.
ПрограМиша начал что-то записывать на листочке и заодно рассуждать вслух:
— Так, нальем ровно 5 литров в пятилитровое ведро – это уж мы можем. Потом перельем из него в трехлитровое 3 литра… О! Кажется, понял! Ведь я же тогда получу ровно 2 литра! А потом я смогу сделать еще раз то же самое, получу еще два литра – вот и будет 4 литра!
— Жаль тебя огорчать, но так не получится, ведь первые два литра тебе некуда перелить, ничего кроме этих двух ведер нету. А оставить два литра в одном из этих двух ведер тоже не получится – они оба нужны, чтобы получить новые два литра. Если бы у тебя была какая-то третья емкость, куда эти два литра можно было бы временно перелить, все бы получилось. Но ее нет. Однако ты на правильном пути! Попробуй еще!
— ПрограМиша, а что если 2 литра, которые ты уже получил, перелить снова в трехлитровое ведро? – МатеМаша задумчиво нарисовала ведра.
— Точно! Тогда я снова наберу полное пятилитровое ведро, перелью из него в трехлитровое столько, сколько поместится, то есть один литр, и в пятилитровом ведре останется ровно 4 литра! – ПрограМиша начал пританцовывать от радости, превратив воображаемое ведро в воображаемый барабан и выстукивая на нем победные марши.
— Молодцы! – я была очень рада, что ребята справились с задачкой. – А теперь давайте запишем решение в виде такой таблички:

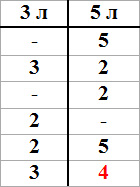
А вам еще одна похожая задачка:

Задача 2.
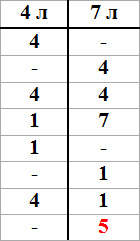
Есть два ведра емкостью 4 литра и 7 литров. С помощью этих ведер нужно набрать из речки ровно 5 литров воды.

МатеМаша с ПрограМишей склонились над листочками и начали рисовать похожие таблички.
— Получилось! – первым закричал ПрограМиша.
— И у меня! – буквально через полминуты радостно воскликнула МатеМаша.
— Давайте дадим подумать и нашим читателям, — предложила я, — а вам, шустрые мои, вот еще одна задачка, подумайте над ней дома:

Задача 3.
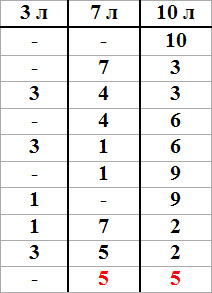
Есть три сосуда: 3 литра, 7 литров и 10 литров. Десятилитровый сосуд полностью заполнен водой, а два других пусты. Нужно перелить воду так, чтобы в двух сосудах оказалось ровно по 5 литров воды.

— А что, тут у нас нет речки? Или хоть какого-то крана с водой? – удивленно спросил ПрограМиша.
— Совершенно верно, нету, — подтвердила я.
— Значит, нам во время переливаний нельзя ни капельки выливать на землю. Ведь в конце должно остаться тоже 10 литров, как и было в самом начале, — рассудительно добавила практичная МатеМаша.
— Очень правильно подмечено, – похвалила я МатеМашу, — а сейчас бегите по домам.
— Я сегодня же обязательно решу эту задачку! – крикнул ПрограМиша, уже спускаясь по лестнице.
— Даже не сомневаюсь! Приходите снова, друзья мои!